In this article I will explain how I solved lagalopex crackme from crackmes.de.You can download my keygen and its source code from here.
These are the rules and information:
Get a working keygen.
Allowed are only GPLed-tools.
Patching/Hijacking prohibited ;)
Difficulty: 3 – Getting harder
Platform: Unix/linux etc.
Language: C/C++
Ok, first let’s execute it to see what’s going on and if we are prompted for something:
daniel@gargamel:~/crackme/lagalopex$ ./cm3
Your name: daniel
Hello daniel, lets see what you've done so far...
daniel@gargamel:~/crackme/lagalopex$
Ok, we have done nothing so far so we cannot expect anything else. If we test the binary with the ‘file’ command we will see that it is not stripped so we might get some useful information from its ‘nm’ and ‘strings’ output:
daniel@gargamel:~/crackme/lagalopex$ nm cm3
0804bf58 T gcd1
0804bf92 T gcd2
0804bfcc T gcd3
0804bea6 T gcd_
U getline@@GLIBC_2.0
U getppid@@GLIBC_2.0
U getpwuid@@GLIBC_2.0
U getsid@@GLIBC_2.0
U getuid@@GLIBC_2.0
0804c007 T gs
0804c0ee T main
U memcpy@@GLIBC_2.0
U open@@GLIBC_2.0
U printf@@GLIBC_2.0
U pthread_attr_destroy@@GLIBC_2.0
U pthread_attr_init@@GLIBC_2.1
U pthread_attr_setdetachstate@@GLIBC_2.0
U pthread_create@@GLIBC_2.1
U pthread_exit@@GLIBC_2.0
U pthread_join@@GLIBC_2.0
U puts@@GLIBC_2.0
0804c03d T rad
0804bf04 T rad_
0804c086 T calc
0804bc34 t rmd160_final
0804be4a T rmd160_hash_buffer
080488b4 t rmd160_init
080488fe t rmd160_trans
0804bb15 t rmd160_write
daniel@gargamel:~/crackme/lagalopex$ strings cm3
[...]
Get a name first...
Hello %s, lets see what you've done so far...
%s/.key_%s
%s/.key_%s_%i
Nice, you got it!
I didn’t list all of them but the interesting ones. We can see that there are threads involved which will probably make our reversing job harder. Also, we can see the presumably goodboy string: ‘Nice, you got it’ and some print format strings. I will not go much in detail with the reversing process and I will just show a flow diagram:

As you can see in the flow diagram, it first computes a hash value of 20 bytes (RIPEMD-160) and then iterates over it through some calculations performed by 6 threads (hence, a total of 120 threads are created). I will describe briefly what these threads do:
- gcd1
0804bf58 gcd1:
804bf58: 55 push ebp
804bf59: 89 e5 mov ebp,esp
804bf5b: 83 ec 08 sub esp,0x8
804bf5e: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804bf61: 8b 50 04 mov edx,DWORD PTR [eax+4]
804bf64: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804bf67: 8b 00 mov eax,DWORD PTR [eax]
804bf69: 89 54 24 04 mov DWORD PTR [esp+4],edx
804bf6d: 89 04 24 mov DWORD PTR [esp],eax
804bf70: e8 31 ff ff ff call gcd_
804bf75: 83 f8 01 cmp eax,0x1
804bf78: 75 0c jne 804bf86
804bf7a: c7 04 24 01 00 00 00 mov DWORD PTR [esp],0x1
804bf81: e8 5e c7 ff ff call pthread_exit
804bf86: c7 04 24 00 00 00 00 mov DWORD PTR [esp],0x0
804bf8d: e8 52 c7 ff ff call pthread_exit
In this code you can see a pointer to a vector holding Xi, Yi and (Xi+Yi). So, as you can see this thread is computing the greatest common divisor of Xi and Yi. If this value is 1 (ie, they are coprimes), then the thread will return 1. Otherwise, the returned value will be zero.
- gcd2
0804bf92 gcd2:
804bf92: 55 push ebp
804bf93: 89 e5 mov ebp,esp
804bf95: 83 ec 08 sub esp,0x8
804bf98: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804bf9b: 8b 50 08 mov edx,DWORD PTR [eax+8]
804bf9e: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804bfa1: 8b 00 mov eax,DWORD PTR [eax]
804bfa3: 89 54 24 04 mov DWORD PTR [esp+4],edx
804bfa7: 89 04 24 mov DWORD PTR [esp],eax
804bfaa: e8 f7 fe ff ff call gcd_
804bfaf: 83 f8 01 cmp eax,0x1
804bfb2: 75 0c jne 804bfc0
804bfb4: c7 04 24 01 00 00 00 mov DWORD PTR [esp],0x1
804bfbb: e8 24 c7 ff ff call pthread_exit
804bfc0: c7 04 24 00 00 00 00 mov DWORD PTR [esp],0x0
804bfc7: e8 18 c7 ff ff call pthread_exit
This thread will compute gcd(Xi,Xi+Yi), ie, the first and the third elements of our vector. If again they are coprimes, the thread will return 1; zero otherwise.
- gcd3
0804bfcc gcd3:
804bfcc: 55 push ebp
804bfcd: 89 e5 mov ebp,esp
804bfcf: 83 ec 08 sub esp,0x8
804bfd2: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804bfd5: 8b 50 08 mov edx,DWORD PTR [eax+8]
804bfd8: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804bfdb: 8b 40 04 mov eax,DWORD PTR [eax+4]
804bfde: 89 54 24 04 mov DWORD PTR [esp+4],edx
804bfe2: 89 04 24 mov DWORD PTR [esp],eax
804bfe5: e8 bc fe ff ff call gcd_
804bfea: 83 f8 01 cmp eax,0x1
804bfed: 75 0c jne 804bffb
804bfef: c7 04 24 01 00 00 00 mov DWORD PTR [esp],0x1
804bff6: e8 e9 c6 ff ff call pthread_exit
804bffb: c7 04 24 00 00 00 00 mov DWORD PTR [esp],0x0
804c002: e8 dd c6 ff ff call pthread_exit
This thread will compute gcd(Yi,Xi+Yi), ie, the second and the third elements of our vector. If again they are coprimes, the thread will return 1; zero otherwise.
- gs
0804c007 gs:
804c007: 55 push ebp
804c008: 89 e5 mov ebp,esp
804c00a: 83 ec 08 sub esp,0x8
804c00d: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804c010: 8b 00 mov eax,DWORD PTR [eax]
804c012: 85 c0 test eax,eax
804c014: 7e 1b jle 804c031
804c016: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804c019: 8b 50 04 mov edx,DWORD PTR [eax+4]
804c01c: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804c01f: 8b 00 mov eax,DWORD PTR [eax]
804c021: 39 c2 cmp edx,eax
804c023: 7e 0c jle 804c031
804c025: c7 04 24 01 00 00 00 mov DWORD PTR [esp],0x1
804c02c: e8 b3 c6 ff ff call pthread_exit
804c031: c7 04 24 00 00 00 00 mov DWORD PTR [esp],0x0
804c038: e8 a7 c6 ff ff call pthread_exit
This thread will return 1 when Xi > Yi and zero otherwise.
- rad
0804c03d rad:
804c03d: 55 push ebp
804c03e: 89 e5 mov ebp,esp
804c040: 83 ec 08 sub esp,0x8
804c043: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804c046: 8b 10 mov edx,DWORD PTR [eax]
804c048: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804c04b: 8b 40 04 mov eax,DWORD PTR [eax+4]
804c04e: 0f af d0 imul edx,eax
804c051: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804c054: 8b 40 08 mov eax,DWORD PTR [eax+8]
804c057: 0f af c2 imul eax,edx
804c05a: 89 04 24 mov DWORD PTR [esp],eax
804c05d: e8 a2 fe ff ff call rad_
804c062: 89 c2 mov edx,eax
804c064: 8b 45 08 mov eax,DWORD PTR [ebp+8]
804c067: 8b 40 08 mov eax,DWORD PTR [eax+8]
804c06a: 39 c2 cmp edx,eax
804c06c: 7d 0c jge 804c07a
804c06e: c7 04 24 01 00 00 00 mov DWORD PTR [esp],0x1
804c075: e8 6a c6 ff ff call pthread_exit
804c07a: c7 04 24 00 00 00 00 mov DWORD PTR [esp],0x0
804c081: e8 5e c6 ff ff call pthread_exit
This thread will calculate the radical of (Xi*Yi*(Xi+Yi)) and if it’s less than (Xi+Yi) it will return 1.
- calc
0804c086 calc:
804c086: push ebp
804c087: mov ebp,esp
804c089: push ebx
804c08a: sub esp,0x14
804c08d: mov eax,DWORD PTR [ebp+8]
804c090: mov ecx,DWORD PTR [eax]
804c092: mov DWORD PTR [ebp-8],0x6bca1af3
804c099: mov eax,DWORD PTR [ebp-8]
804c09c: imul ecx
804c09e: sar edx,0x3
804c0a1: mov eax,ecx
804c0a3: sar eax,0x1f
804c0a6: mov ebx,edx
804c0a8: sub ebx,eax
804c0aa: mov eax,DWORD PTR [ebp+8]
804c0ad: mov ecx,DWORD PTR [eax+4]
804c0b0: mov DWORD PTR [ebp-8],0xae4c415d
804c0b7: mov eax,DWORD PTR [ebp-8]
804c0ba: imul ecx
804c0bc: lea eax,[edx+ecx]
804c0bf: mov edx,eax
804c0c1: sar edx,0x6
804c0c4: mov eax,ecx
804c0c6: sar eax,0x1f
804c0c9: mov ecx,edx
804c0cb: sub ecx,eax
804c0cd: mov eax,ecx
804c0cf: lea edx,[ebx+eax]
804c0d2: mov eax,edx
804c0d4: sar eax,0x1f
804c0d7: mov ecx,eax
804c0d9: shr ecx,0x18
804c0dc: lea eax,[edx+ecx]
804c0df: and eax,0xff
804c0e4: sub eax,ecx
804c0e6: mov DWORD PTR [esp],eax
804c0e9: call pthread_exit
Now we have to find out what this function does since, at first glance, it’s not as simple as the other ones.
It makes some operations with the first and second values of our vector, ie, Xi and Yi. And right before the call to pthread_exit instruction we can see that the returned value is AND’ed with 0xFF so the output of this function will be between 0x00 and 0xFF. I will not dig too much into all the shifts and the multiplications details; instead I will print its equivalent C source.
int calc(int *v)
{
int x, y;
x=v[0];
y=v[1];
return ( ((int)(x/19) + (int)(y/94)) % 256 );
}
Now let’s have a look at the way the binary is collecting all this data and how it is processed:
804c677: call 80486c4
804c67c: test eax,eax
804c67e: je 804c68f
804c680: mov DWORD PTR [ebp-0x2510],0x3
804c687:
804c68a: jmp 804c869
804c68f: mov eax,DWORD PTR [ebp-0x360]
804c695: add DWORD PTR [ebp-20],eax
This is the code which actually collects the data returned by the ‘gcd1 threads’. Essentially it does the same than the ‘gcd2’, ‘gcd3’, ‘gs’, and ‘rad’ threads so I will just comment this one.
After the call to pthread_join, the returned value is at [ebp-0x360] address. If it is not zero (ie, if it is 1), the value is added to the value at [ebp-0x360] which is the counter shown in the flow chart.
Let’s now analyze the ‘pthread_join’ to the ‘calc’ threads:
804c7f8: call pthread_join
804c7fd: test eax,eax
804c7ff: je 804c80d
804c801: mov DWORD PTR [ebp-0x2510],0x3
804c808:
804c80b: jmp 804c869
804c80d: mov eax,DWORD PTR [ebp-24]
804c810: movzx eax,BYTE PTR [ebp+eax-0x24fc]
804c817:
804c818: movsx eax,al
804c81b: movzx edx,al
804c81e: mov eax,DWORD PTR [ebp-0x360]
804c824: cmp edx,eax
804c826: je 804c834
804c828: mov DWORD PTR [ebp-0x2510],0x5
804c82f:
804c832: jmp 804c869
804c869: mov eax,DWORD PTR [ebp-0x2510]
804c86f: add esp,0x252c
804c875: pop ecx
804c876: pop ebx
804c877: pop edi
804c878: leave
804c879: lea esp,[ecx-4]
804c87c: ret
This code gets the value returned from the ‘calc’ thread and compares it to the H[i] which holds the i-th hash value. If they don’t match, the program will exit with code 5. Otherwise, it will continue picking up the values returned by the threads. So for the sake of writing the keygen we now know that the (Xi,Yi) values read from the file must satisfy this constraint. If not, the program will just exit without printing out the goodboy message.
After all the exit values are collected and processed we will find the following code:
804c841: 8b 5d ec mov ebx,DWORD PTR [ebp-20]
804c844: 83 eb 64 sub ebx,0x64
804c847: e8 78 bf ff ff call rand
804c84c: 0f af c3 imul eax,ebx
804c84f: 85 c0 test eax,eax
804c851: 75 0c jne 804c85f
804c853: c7 04 24 b4 c9 04 08 mov DWORD PTR [esp],0x804c9b4
804c85a: e8 55 bf ff ff call puts
The ‘result’ value is loaded into ebx, then 0x64 is substracted from it and multiplied by a random value.
If the multiplication returns zero, the goodboy string is moved onto the stack and printed out through puts function:
if( (counter-0x64) * rand() == 0)
puts("Nice, you got it!");
The way to go is making ‘counter’ to be 0x64. In every iteration, counter is incremented by 5 if the conditions are satisfied; as there are 20 iterations, counter will be 100 (0x64) if (Xi,Yi) pairs are correctly chosen. And this is what our keygen should do.
Putting it all together:

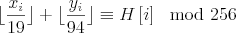


To get a working keygen, we must implement a sort of intelligent brute-force keeping in mind all the constraints listed above.
- ABC Conjecture
This conjecture was first put forward in 1980 by Joseph Oesterle of the University of Paris and David Masser of the Mathematics Institute of the University of Basel in Switzerland, which is now considered one of the most important unsolved problems in number theory. This conjecture deals with numbers that have no common factors. For example, if A=3 and B=7 then we’ll have C=10. These 3 numbers are relative primes but rad(A*B*C) > C. Occasionally this is not always true; for instance, if A=1 and B=8, then C=9, rad(A*B*C)=1*2*3=6 < 9.
From here we can read:
If rad(a*b*c) can be less than c, just how much less? Can we find an example where rad(abc) is so much smaller that the square of rad(abc) is also less than c? No one knows of such a triple, but there are some examples where [rad(abc)]α < c for some exponent α greater than 1 though less than 2. Take the triple {2, 6436341, 6436343}. Here b is equal to 310 × 109 and c is equal to 235, and so rad(abc) = 2 × 3 × 23 × 109 = 15042. And 15042α < 6436343 for any α < 1.6299.
In 1985 Joseph Oesterlé of the University of Paris and David W. Masser of the University of Basel conjectured that there are only finitely many such exceptional triples. Given a positive number ε that can be made arbitrarily small, [rad(abc)]1 + ε can be less than c only in a finite number of cases (which will depend on ε). That’s the abc conjecture.
First of all we should try only the (Xi,Yi) pairs so that calc(Xi,Yi) = H(i); to achieve this we need a way to solve that equation:
int solve_calc(int x, int k)
{
int d = k - (int)(x/19);
return d*94;
}
We will get the Yi candidates by solving the equation with some Xi and the H[i] value for each iteration. The ‘solve_calc’ function will return a valid Yi but it’s not the only one which will satisfy the ‘calc’ condition. Valids Yi will range from the returned value to the returned value+93 and we can add them n*256 (for any positive n) since the calc function performs a modulo 256 operation.
As well, for each Xi value multiple of 19, we will get the same ‘calc’ value for the next 18 ones due to the integer division.
With these in mind we now have to bruteforce the obtained pairs to find the ones who satisfy the co-primality and radical restrictions. The way I will deal with the co-primality restrictions is by computing the GCD with the Extended Euclidean Algorithm. However, the hardest part is computing the radical of the numbers since a factorization is needed.
To speed the factorization process up I will use the Sieve of Eratosthenes to compute a table with all the primes up to a limit.
Please, have a look at the source code of the keygen for a further understanding of the process I have described. In a Pentium 4 3.0 GHz a valid license is generated in less than 1 second but it also depends on the hash value.
daniel@gargamel:~/crackme/lagalopex$ time ./keygen
Username: daniel
Sieve of Eratosthenes Prime Generation...OK
100% completed
Writing license info into /home/daniel/.key_daniel
real 0m1.079s
user 0m0.420s
sys 0m0.030s
As you can see it took about 0.45 seconds to generate the numbers and write the license file. The rest of the time is how much it took me to write my username :-).
daniel@gargamel:~/crackme/lagalopex$ time ./cm3
Your name: daniel
Hello daniel, lets see what you've done so far...
Nice, you got it!
real 0m1.711s
user 0m1.020s
sys 0m0.030s
Voila ! We got a working keygen and it takes less than half the time in the bruteforcing process than the crackme itself in verifying our license.
Notes:
Regarding the string to be hashed I’d like to point out that the final part of it is a number of value: getppid()-getsid(). This number should be zero since the parent PID and the session ID are the same if the program is running from a shell. However if you are debugging the crackme (gdb, strace, ltrace, …) the parent process ID will be the PID of the debugger and this assumption is not true anymore. To debug the program with the data generated by my KeyGen I made a little trick based on LD_PRELOAD so that getppid and getsid always return 0:
int getppid() { return 0; }
int getsid(int pid) { return 0; }
gcc -shared -o fakeids.so fakeids.c
export LD_PRELOAD=$PWD/fakeids.so
daniel@gargamel:~/crackme/lagalopex$ ./testuids
ppid()=0
getsid()=0
This way, the debugging process becomes easier.
Hope you found this article interesting.
Regards,
Daniel




