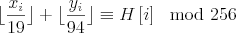In this tutorial I will explain how to solve a crackme rated level 4 at crackmes.de from DrSpliff which I found very interesting.
You can download the original author’s file from here.
You can download both the original file and the patched one created by me from here.
The readme file says:
This crackme uses the basic principals and building blocks of software protection on Unix systems with a little bit of crypto thrown in to piss you off.
Difficulty: 4 – Needs special knowledge
Platform: Unix/linux etc.
Language: C/C++
_________________
Actually this is not a Linux dependent crackme since it’s got no specific Unix/Linux protections but it was compiled for it though.
First thing we do is executing the binary (although I trust crackmes.de I use to have a quick look at the binaries to avoid malicious code being executed on my machine).
daniel@gargamel:~/crackme$ ./drscm1
Dr.Spliff's Crackme - v0.1 (Alpha) (Linux/ia32)
Name: daniel
Serial: 123
Sorry daniel, your license is invalid
Having a quick look at the binary and loading it into gdb it seems that the author’s not used any antidebugging techniques nor ELF header corruption so we can freely analyze / disassemble it.
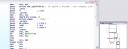 First I opened it with IDA (my favourite disassembler. It’s for Windows but you can run it under wine) to analyze the program flow with its nice Graph View. Quickly I can see where in the code it reads our name / serial (see image).
First I opened it with IDA (my favourite disassembler. It’s for Windows but you can run it under wine) to analyze the program flow with its nice Graph View. Quickly I can see where in the code it reads our name / serial (see image).
After this, some memory is allocated via malloc and a buffer is copied into it. This buffer is 56 bytes long and it’s located at address 0x8049a20 (this may change in your computer). After the copy, this buffer is modified somehow by this piece of code:
At the beggining of the loop, edi is pointing to our buffer and it’s being processed in blocks of 8 bytes (64 bits).
.text:08048742 push edi
.text:08048743 add edi, 8
.text:08048746 push offset 08049A5C
.text:0804874B call sub_080485AF
.text:08048750 add [ebp+var_410], 8
.text:08048757 pop eax
.text:08048758 pop edx
.text:08048759 movsx eax, byte_8049A58
.text:08048760 cmp [ebp+var_410], eax
.text:08048766 jl short loc_8048742
If we look further into sub_080485AF, we can identify its main loop with a ‘suspicious’ structure:
.text:080485DB mov edx, ecx
.text:080485DD lea eax, [esi+ecx]
.text:080485E0 shl edx, 4
.text:080485E3 add edx, [ebp+var_14]
.text:080485E6 xor edx, eax
.text:080485E8 mov eax, ecx
.text:080485EA shr eax, 5
.text:080485ED add eax, [ebp+var_18]
.text:080485F0 xor edx, eax
.text:080485F2 sub ebx, edx
.text:080485F4 mov edx, ebx
.text:080485F6 shl edx, 4
.text:080485F9 lea eax, [esi+ebx]
.text:080485FC add edx, [edi]
.text:080485FE add esi, 61C88647h
.text:08048604 xor edx, eax
.text:08048606 mov eax, ebx
.text:08048608 shr eax, 5
.text:0804860B add eax, [edi+4]
.text:0804860E xor edx, eax
.text:08048610 sub ecx, edx
.text:08048612 dec [ebp+var_10]
.text:08048615 jns short loc_80485DB
Notice the 4-bit shifts to the left and the 5-bit shifts to the right. It looks familiar… hmm, maybe TEA? That’s it! Having a look at a public implementation of TEA algorithm we can say for sure it is and this is actually the decoding function. If this is the decoding function, the key used shouldn’t be too far away and the stack is a good place to look at first. Indeed, it’s there and it looks like it’s been hardcoded by the author (at least there are no x-refs to it).
Okay, let’s go along the code and see what happens after all this crypto stuff. We find this piece of code:
.text:08048768 push 0 ; prot
.text:0804876A movsx eax, byte_8049A58
.text:08048771 push eax ; len
.text:08048772 push ds:addr ; addr
.text:08048778 call _mprotect
.text:0804877D push offset sub_804855B
.text:08048782 push offset sub_80484FC
.text:08048787 push ebx
.text:08048788 call ds:addr
Interesting huh? The address at ‘ds:addr’ is actually our decrypted buffer. The mprotect function call is used to set protection of a memory mapping and as we can see in the code above the protection argument is zero or (PROT_NONE) to allow execution of the memory which is about to be executed in the ‘call ds:addr’ instruction.
The arguments of the function which is supposed to be in ‘ds:addr’ are two procedures: sub_804855B and sub_80484FC. Clearly these procedures are the ‘bad and good’ boys. I could try to change the code so that the good boy address is pushed twice onto the stack but the function at ‘ds:addr’ could check that the two parameters are distinct and this wouldn’t be a real crack 🙂 I’d like to dig more into the executable to find out what the author really pretended.
So, the way to go is to load the executable with GDB and break just after the data is already decrypted so that we can analyze what it really holds:
(gdb) x/56i *0x8049b8c
0x804a028: push %ebp
0x804a029: mov %esp,%ebp
0x804a02b: push %esi
0x804a02c: sub $0x4,%esp
0x804a02f: mov 0x8(%ebp),%esi ; take a ptr to a ptr to the name
0x804a032: mov $0x0,%ecx ; ecx = 0
0x804a037: mov (%esi),%edx ; edx = ptr to the name
0x804a039: cmpb $0x0,(%edx) ; compare ''
0x804a03c: je 0x804a049 ; if string's finished jump to 0x804a049
loop:
0x804a03e: movsbl (%edx),%eax ; eax = name[i]
0x804a041: add %eax,%ecx ; ecx += name[i]
0x804a043: inc %edx ; ptr++
0x804a044: cmpb $0x0,(%edx) ; name[i] == '' ?
0x804a047: jne 0x804a03e ; no -> jump to loop
0x804a049: cmp 0x4(%esi),%ecx ; compare with the serial when string's fully proccessed
end_loop:
0x804a04c: jne 0x804a057 ; if we nop this jump, then we'll always have the goodboy
0x804a04e: sub $0xc,%esp
0x804a051: push %esi
0x804a052: call *0xc(%ebp) ; call good boy
0x804a055: nop
0x804a056: nop
0x804a057: sub $0xc,%esp
0x804a05a: push %esi
0x804a05b: call *0x10(%ebp) ; call bad boy
0x804a05e: nop
0x804a05f: nop
The good boy is at ebp+0x0C and the bad boy at ebp+0x10C. The routine performs a simple algorithm and then compares the result to the serial we entered. If they match, then we’ll have the good boy. We can see that writing a keygen is pretty easy now and that’s why I won’t do it.
So, by simply nopping the ‘jne 0x804a057’ instruction located at 0x804a04c we’ll get the application to show the good boy no matter whether the serial is right or not. To do this we have to dump these 56 bytes, patch and re-cypher them using TEA with the same key.
Key used by the executable for decryption:
TEA_Key
db 75h, 8, 0D3h, 16h, 0D1h, 3, 0Eh, 0 ; 0
db 0E5h, 2Bh, 96h, 0, 8Fh, 45h, 1Eh, 0 ; 8
TEA cyphered data:
.data:08049A20 db 0Ch, 26h, 0F5h, 42h, 0A3h, 0ACh, 0D3h, 3Ch; 0
.data:08049A20 db 0DCh, 0B3h, 86h, 0B2h, 4Bh, 0C5h, 3Ch, 29h; 8
.data:08049A20 db 88h, 66h, 49h, 73h, 0A4h, 0CFh, 7Bh, 0B1h; 16
.data:08049A20 db 3Ah, 5Bh, 0CBh, 37h, 0BDh, 2Ah, 35h, 0FCh; 24
.data:08049A20 db 95h, 0E7h, 0E8h, 0BAh, 2Bh, 66h, 67h, 0BCh; 32
.data:08049A20 db 2Dh, 0AFh, 34h, 32h, 2Eh, 5Bh, 0C1h, 0Eh; 40
.data:08049A20 db 1Eh, 0FAh, 8Eh, 63h, 6Dh, 0C1h, 51h, 78h; 48
Putting this all together we need a TEA implementation. I will use the following source code:
void code(long *v, long *k)
{ unsigned long y = v[0],
z = v[1],
sum = 0, /* set up */
delta = 0x9e3779b9,
n = 32,
a = k[0],
b = k[1],
c = k[2],
d = k[3];
while (n-- > 0) /* basic cycle start */
{ sum += delta;
y += (z <> 5) + b;
z += (y <> 5) + d; /* end cycle */
}
v[0] = y;
v[1] = z;
}
void decode(long *v, long *k)
{ unsigned long n = 32,
sum,
y = v[0],
z = v[1],
delta = 0x9e3779b9,
a = k[0],
b = k[1],
c = k[2],
d = k[3];
sum = delta < 0)
{ z -= (y <> 5) + d;
y -= (z <> 5) + b;
sum -= delta;
}
/* end cycle */
v[0] = y;
v[1] = z;
}
int main(int argc, char **argv)
{
long cyphered[] = {0x42F5260C, 0x3CD3ACA3, 0x0B286B3DC, 0x293CC54B, 0x73496688, 0x0B17BCFA4, 0x37CB5B3A, 0x0FC352ABD, 0x0BAE8E795, 0x0BC67662B, 0x3234AF2D, 0x0EC15B2E, 0x638EFA1E, 0x7851C16D };
long key[] = { 0x16D30875, 0x0E03D1, 0x962BE5, 0x1E458F };
long *ptrc;
int i;
ptrc=cyphered;
for(i=0;i<7;i++)
{
decode((unsigned long *)ptrc, (unsigned long *)key);
ptrc+=2;
}
return 1;
}
Executing this code we will get our buffer decrypted (we could have got this data by debugging the executable itself but this way we are also checking that everything is going all right). Having a look at the ‘cyphered’ buffer with gdb on the above program:
(gdb) p/x cyphered
{0x56e58955, 0x8b04ec83, 0xb90875, 0x8b000000,
0x3a8016, 0xbe0f0b74, 0x42c10102, 0x75003a80,
0x44e3bf5, 0xec830975, 0x55ff560c, 0x8390900c,
0xff560cec, 0x90901055}
Okay here is the decyphered buffer with actually holds the code executed by our binary. It contains the jnz to be nopped by us so we can clearly identify the JNZ opcodes (0x0975) which should be changed by two NOP’s (0x9090) and the buffer would look like this:
{0x56e58955, 0x8b04ec83, 0xb90875, 0x8b000000,
0x3a8016, 0xbe0f0b74, 0x42c10102, 0x75003a80,
0x44e3bf5, 0xec839090, 0x55ff560c, 0x8390900c,
0xff560cec, 0x90901055}
So now it’s time to cypher this data using the same key so that when our program decrypts it, we always get the good boy.
int main(int argc, char **argv)
{long decyphered[] = { 0x56e58955, 0x8b04ec83, 0xb90875, 0x8b000000,0x3a8016, 0xbe0f0b74, 0x42c10102, 0x75003a80,0x44e3bf5, 0xec839090, 0x55ff560c, 0x8390900c,0xff560cec, 0x90901055 };
long key[] = { 0x16D30875, 0x0E03D1, 0x962BE5, 0x1E458F };
long *ptrd;
char *ptr;
int i;
ptrd=decyphered;
for(i=0;i<7;i++)
{
code((unsigned long *)ptrd, (unsigned long *)key);
ptrd+=2;
}
ptr=(char*)decyphered;
for(i=0;i<56;i++)
printf("%02X,",ptr[i]);
return 1;
}
The output of this program:
0x0C, 0x26, 0xF5, 0x42, 0xA3, 0xAC, 0xD3, 0x3C,
0xDC, 0xB3, 0x86, 0xB2, 0x4B, 0xC5, 0x3C, 0x29,
0x88, 0x66, 0x49, 0x73, 0xA4, 0xCF, 0x7B, 0xB1,
0x3A, 0x5B, 0xCB, 0x37, 0xBD, 0x2A, 0x35, 0xFC,
0x05, 0x51, 0x3F, 0xE3, 0xCF, 0x7F, 0x2D, 0x78,
0x2D, 0xAF, 0x34, 0x32, 0x2E, 0x5B, 0xC1, 0x0E,
0x1E, 0xFA, 0x8E, 0x63, 0x6D, 0xC1, 0x51, 0x78,
Actually the only block (8 bytes long) which has changed’s been obviously the one containing the NOP’ed JNZ so its bytes are to be substituted in the original binary file. We open it with our favourite hex-editor and patch the file.
Once we’ve patched the file it’s time to try and see what’s going on after all this job:
daniel@gargamel:~/crackme$ ./drscm1-patched
Dr.Spliff's Crackme - v0.1 (Alpha) (Linux/ia32)
Name: daniel
Serial: 123
Congrats daniel, your license is valid
Now, go post your solution on crackmes.de so others can learn
daniel@gargamel:~/crackme$ ./drscm1-patched
Dr.Spliff's Crackme - v0.1 (Alpha) (Linux/ia32)
Name: dani
Serial: 4535
Congrats dani, your license is valid
Now, go post your solution on crackmes.de so others can learn
daniel@gargamel:~/crackme$ ./drscm1-patched
Dr.Spliff's Crackme - v0.1 (Alpha) (Linux/ia32)
Name: aa
Serial: 194
Congrats aa, your license is valid
Great ! It worked! Now let’s have a look at the modified code to see how it looks like after the patch:
(gdb) x/24i 0x804a028
0x804a028: push %ebp
0x804a029: mov %esp,%ebp
0x804a02b: push %esi
0x804a02c: sub $0x4,%esp
0x804a02f: mov 0x8(%ebp),%esi
0x804a032: mov $0x0,%ecx
0x804a037: mov (%esi),%edx
0x804a039: cmpb $0x0,(%edx)
0x804a03c: je 0x804a049
0x804a03e: movsbl (%edx),%eax
0x804a041: add %eax,%ecx
0x804a043: inc %edx
0x804a044: cmpb $0x0,(%edx)
0x804a047: jne 0x804a03e
0x804a049: cmp 0x4(%esi),%ecx
0x804a04c: nop <---- Our NOP-ed JNZ
0x804a04d: nop <---- Our NOP-ed JNZ
0x804a04e: sub $0xc,%esp
0x804a051: push %esi
0x804a052: call *0xc(%ebp) <---- Always call the good boy
0x804a055: nop
This is the hardest part of the crackme. However we assumed for simplicity that the serial entered is a number. However the program checks the return of an atoi() call to the serial. If atoi fails then the ‘Invalid serial’ message appears. To avoid this, just patch the jne after the atoi call and replace it by an unconditional jump:
80486d8: jne 0x80486f8
Open the file with an hexeditor and change the 0x75 (JNE opcode) byte at 0x6d8 by a 0xEB (JMP opcode).
Also, the program performs a check to the length of the input name:
or edx, 0FFFFFFFFh
xor eax, eax
cld
mov ecx, edx
repne scasb
not ecx
dec ecx
cmp ecx, 1
ja short loc_804869A
This is a typical ‘strlen’ and the jump to 0x804869A is taken just if the length of the name is > 0.
So if we want to skip this restriction, we could patch the JA opcode the same way: Replacing the 0x77 (JA) byte at 0x68C offset of the file by a 0xEB (JMP).
The End.
Hope you enjoyed this article and found it useful.
Regards,
Daniel
 DIEZ is a line following robot which has been designed for several national contests being held in Spain throughout the year.
DIEZ is a line following robot which has been designed for several national contests being held in Spain throughout the year. been developed to test and debug the algorithm before coding it into the microcontroller. Here you can see an screenshot of this program which allowed us to monitor in Real Time what the robot saw in every moment. Also, thanks to the SD socket of the LPC2138-01 board, the robot was recording all the data and parameters on it for a later study with this program. This was specially useful to detect some of the problems of the algorithm because we had all the telemetry. This recording was quite feasible using the Embedded File System Library since the robot just had to create a new telemetry file on a FAT32 filesystem which was perefctly readable from any computer.
been developed to test and debug the algorithm before coding it into the microcontroller. Here you can see an screenshot of this program which allowed us to monitor in Real Time what the robot saw in every moment. Also, thanks to the SD socket of the LPC2138-01 board, the robot was recording all the data and parameters on it for a later study with this program. This was specially useful to detect some of the problems of the algorithm because we had all the telemetry. This recording was quite feasible using the Embedded File System Library since the robot just had to create a new telemetry file on a FAT32 filesystem which was perefctly readable from any computer.